Example Problems on Set Theory and Probability
ST501 Homework 1 on Set Theory and Probability
Problems: 1.2, 1.4, 1.6 + R Problem
1.2
Two six-sided dice are thrown sequentially, and the face values that come up are recorded.
a.
List the sample space.
\[\begin{align} \Omega = \{ & 11, 12, 13, 14, 15, 16, \\ & 21, 22, 23, 24, 25, 26, \\ & 31, 32, 33, 34, 35, 36, \\ & 41, 42, 43, 44, 45, 46, \\ & 51, 52, 53, 54, 55, 56, \\ & 61, 62, 63, 64, 65, 66 \} \end{align}\]b.
List the elements that make up the following events:
(1)
$A=$ the sum of the two values is at least 5
\[\begin{align} A = \{ & 14, 15, 16, \\ & 23, 24, 25, 26, \\ & 32, 33, 34, 45, 36, \\ & 41, 42, 43, 44, 45, 46, \\ & 51, 52, 53, 54, 55, 56, \\ & 61, 62, 63, 64, 65, 66 \} \end{align}\](2)
$B=$ the value of the first die is higher than the value of the second
\[\begin{align} B = \{ & 21, \\ & 31, 32, \\ & 41, 42, 43, \\ & 51, 52, 53, 54, \\ & 61, 62, 63, 64, 65 \} \end{align}\](3)
$C=$ the first value is 4
\[C = \{ 41, 42, 43, 44, 45, 46 \}\]c.
List the elements of the following events
(1)
$A \cap C$
\[A \cap C = \{41, 42, 43, 44, 45, 46 \}\](2)
$B \cup C$
\[\begin{align} B \cup C = \{ & 21, \\ & 31, 32, \\ & 41, 42, 43, 44, 45, 46, \\ & 51, 52, 53, 54, \\ & 61, 62, 63, 64, 65 \} \end{align}\](3)
$A \cap (B \cup C)$
\[\begin{align} A \cap (B \cup C) = & \\ = & \begin{Bmatrix} 14, & 15, & 16, \\ 23, & 24, & 25, & 26, \\ 32, & 33, & 34, & 45, & 36, \\ 41, & 42, & 43, & 44, & 45, & 46, \\ 51, & 52, & 53, & 54, & 55, & 56, \\ 61, & 62, & 63, & 64, & 65, & 66 \end{Bmatrix} \cap \begin{Bmatrix} \\ 21, \\ 31, & 32, \\ 41, & 42, & 43, & 44, & 45, & 46, \\ 51, & 52, & 53, & 54, \\ 61, & 62, & 63, & 64, & 65 \end{Bmatrix} \\ = & \{ 32, \\ & 41, 42, 43, 44, 45, 46 \\ & 51, 52, 53, 54, \\ & 61, 62, 63, 64, 65 \} \end{align}\]1.4
Draw Venn diagrams to illustrate De Morgan’s laws:
Note: The Red indicates the expressed region.
\[(A \cup B)^{C} = A^{C} \cap B^{C}\]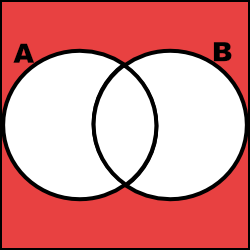
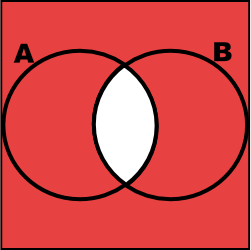
1.6
Verify the following extension of the addition rule (a) by an appropriate Venn diagram and (b) by a formal argument using the axioms of probability and teh propositions in this chapter.
\[P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)\]a.
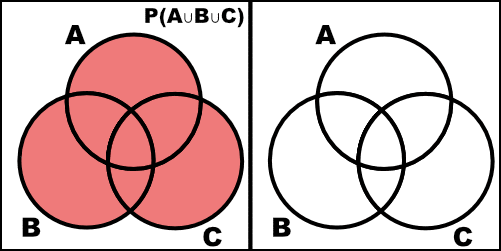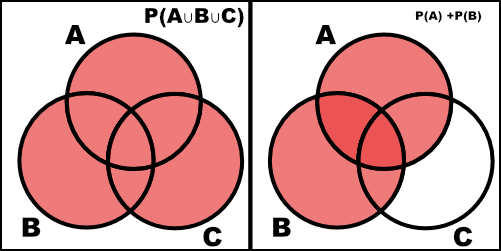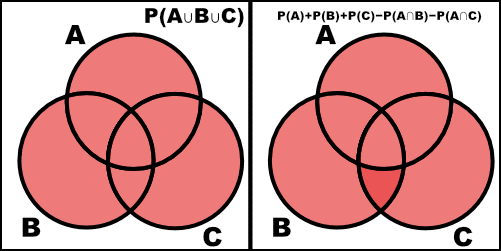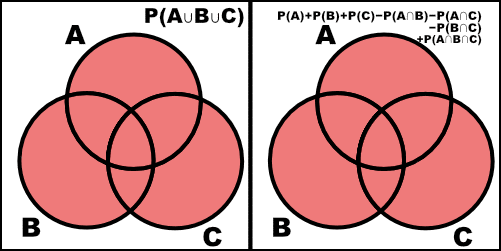
![=]](/img/smile.svg)