Example Problems on Set Theory and Probability
ST701 Homework 1 on Set Theory and Probability
Problems: 1.1, 1.4, 1.5, 1.13, 1.23, Problem 6
1.1
For each of the following experiments, describe the sample space.
a.
Toss a coin four times.
This will look like a sequence of 4 heads or tails. e.g ${HHHH, HHHT, HHTH, \dots TTTT}$. There will be 16 elements.
b.
Count the number of insect damaged leaves on a plant.
This will be the natural numbers, $[0, \infty)$, assuming there is no limit to the possible number of leaves on a plant.
c.
Measure the lifetime (in hours) of a particular brand of light bulb.
This can be any real number greater than or equal to 0, $[0, \infty)$.
d.
Record the weights of 10-day-old rats.
This can be any real number greater than 0, $(0, \infty)$.
e.
Observe the proportion of defectives in a shipment of electronic components.
This can be any real number between 0 and 1, $[0, 1]$.
1.4
For events $A$ and $B$, find formulas for the probabilities of the following events in terms of quantities $P(A)$, $P(B)$, and $P(A\cap B)$.
a.
either in $A$ or $B$ or both
\[\begin{align} P(A\cup B) & = P(A) + P(B) - P(A \cap B) & \text{by theorem 3.2} \end{align}\]b.
either $A$ or $B$ but not both
\[\begin{align} P( (A\cup B) - (A\cap B) ) & = P(A) + P(B) - 2 P(A \cap B) \end{align}\]c.
at least one of $A$ or $B$
\[\begin{align} P(A\cup B) & = P(A) + P(B) - P(A \cap B) & \text{by theorem 3.2} \end{align}\]d.
at most one of $A$ or $B$
\[1-P(A\cap B)\]1.5
Approximately one-third of all human twins are identical (one-egg) and two-thirds are fraternal (two-egg) twins. Identical twins are necessarily the same sex, with male and female being equally likely. Among fraternal twins, approximately one-fourth are both female, one-fourth are both male, and half are one male and one female. Finally, among all U.S. births, approximately 1 in 90 is a twin birth. Define the following events:
\[\begin{align} A = & \text{\{ a U.S. birth results in twin females \}}\\ B = & \text{ \{ a U.S. birth results in identical twins \} } \\ C = & \text{ \{ a U.S. birth results in twins. \} } \end{align}\]a.
State in words, the event $A\cap B \cap C$.
The set of U.S. birth results in female, identical twins. (Notice that $A$ and $B$ are subsets of $C$.)
b.
Find $P(A \cap B \cap C)$.
\[P(A \cap B \cap C) = \frac{ 1 }{ 90 } \cdot \frac{ 1 }{ 3 } \cdot \frac{ 1 }{ 2 } = \frac{ 1 }{ 540 }\]Where
\[\begin{align} \frac{ 1 }{ 90 } = & \text{The proportion of twin births,}\\ \frac{ 1 }{ 3 } = & \text{The proportion of twins that are identical,} \\ \frac{ 1 }{ 2 } = & \text{The proportion of identical twins that are female.} \end{align}\]1.13
If $P(A)=\frac{ 1 }{ 3 }$ and $P(B^C) = \frac{ 1 }{ 4 }$, can $A$ and $B$ be disjoint? Explain.
No, $A$ and $B$ cannot be disjoint. Notice that $P(B) = 1 - P(B^C) = \frac{ 3 }{ 4 }$. If we assume that $A$ and $B$ are disjoint, then $A\cap B = \varnothing$; however $P(A) + P(B) = \frac{ 13 }{ 12 } > 1$. Thus, $A$ and $B$ cannot be disjoint and some elements must be in their intersection.
1.23
Two people each toss a fair coin $n$ times. Find the probability that they will toss the same number of heads. (Answer: $(\frac{ 1 }{ 4 })^n \cdot {2n \choose n}$ )
Notice that the process of flipping a coin is a binomial distribution with $n$ trials and a probability of success $1/2$. Notice that the outcome of each person is indepent of the other. Since we are looking for when they flip the same number of heads we are essentially looking for $P(X=k) \land P(Y=k)$ (where $X$ and $Y$ represent the outcomes of the first and second person respectively). Since these events are independent, we can multiply their CDFs together.
\[\begin{align} \sum_{k=1}^{n} \Big[ {n \choose k} \frac{ 1 }{ 2 }^k \frac{ 1 }{ 2 }^{n-k} \Big] \cdot \Big[ {n \choose k} \frac{ 1 }{ 2 }^k \frac{ 1 }{ 2 }^{n-k} \Big] & = \sum_{k=1}^{n} {n \choose k} {n \choose k} \frac{ 1 }{ 2 }^{2n} \\ & = \frac{ 1 }{ 2 }^{2n} \sum_{k=1}^{n} {n \choose k} {n \choose k} \\ & = \frac{ 1 }{ 2 }^{2n} \cdot {2n \choose n} & \text{by Vandermonde's identity} \\ & = \Big( \frac{ 1 }{ 4 } \Big)^n \cdot {2n \choose n} \end{align}\]6
Prove rigorously that
\[P(A\cup B\cup C) = P(A) + P(B) + P(C) - P(A\cap B) - P(A\cap C) - P(B\cap C) + P(A\cap B\cap C)\](Hint: use $P(A\cup B) = P(A) + P(B) - P(A\cap B)$ and Theorem 1.1.4 in the textbook.) Note Venn diagram is not sufficient for a proof here.
\[\begin{align} P(A \cup B \cup C) & = P(A \cup (B \cup C)) \\ & = P(A) + P(B \cup C) - P(A \cap (B \cup C)) \\ & = P(A) + P(B) + P(C) - P(B \cap C) - P(A \cap (B \cup C)) \\ & = P(A) + P(B) + P(C) - P(B \cap C) - P( (A \cap B) \cup (A \cap C)) \\ & = P(A) + P(B) + P(C) - P(B \cap C) - (P(A \cap B) + P( A \cap C) - P(A \cap B \cap C)) \\ & = P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C) \end{align}\]We can check this with a Venn diagram.
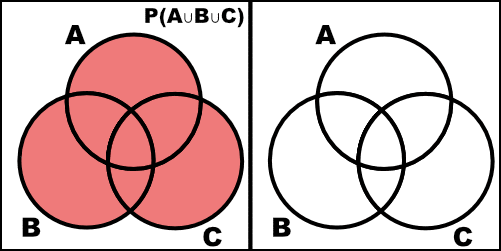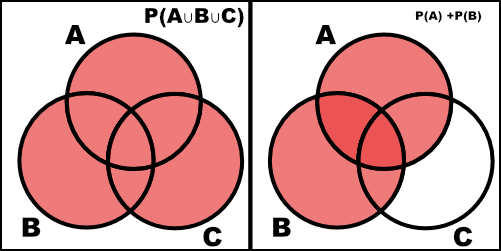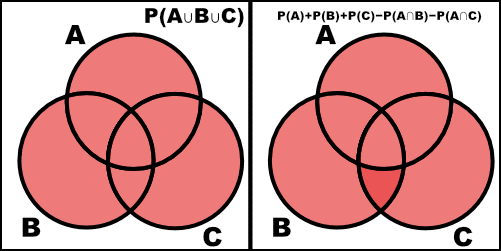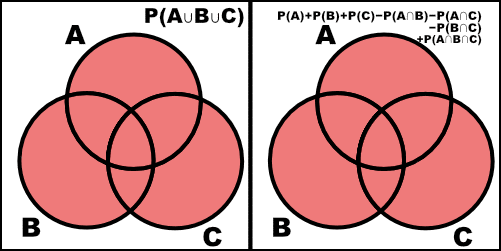
![=]](/img/smile.svg)